Trapez Kaśka: Bardzo proszę W trapez prostokątny wpisano okrąg. Punkt styczności okręgu z dłuższym ramieniem dzieli to rami na odcinki długości 6cm i 24cm. Oblicz obwód trapezu

ICSP: 108

Kaśka: Ale jak to policzyć?

ICSP: Dobrze policzyłem?

Kaśka: taki jest wynik

ICSP: Jaka forma dzisiaj

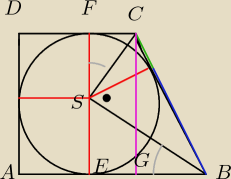ICSP: zielony odcinek ma długość 6 a niebieski ma długość 24. Z tego wynika że czerwony odcinek ma długość 12. Różowy odcinek ma długość dwóch czerwonych czyli 24. teraz odczytujemy częśc |AD| = 24 |AE| = |DF| = 12 |CB| = 30 teraz z twierdzenia Pitagorasa liczymy długość odcinka GB: |GB|² + |GC|² = |BC|² podstawisz i otrzymasz GB = 18 |EG| = x = |FC| podobieństwo trójkątów SFC i SEB:

x		12
	=
12		x+18

x² + 18x − 144 = 0 x musi być dodanie i wychodzi x = 6 Obw = 12 + 6 + 18 + 30 + 6 + 12 + 24 = 108

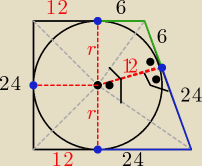Eta: Ob= 108

ICSP: Wiedziałem że musi być jakiś prostszy sposób

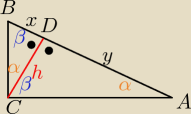Eta: ΔCAD ~ΔCDB

	h		y
to:		=		=> h2= x*y
	x		h

r jest wysokością poprowadzoną z wierzchołka kąta prostego h²= x*y x=6 y=24 to r²= 6*24 =144 => r= 12